Benchmarks and Limitations

Combining Limitations

As I mentioned with Crusher.dm2, some benchmarks have more than one limit, depending on the system, the resolution, and the 3D accelerator used. How do we go about recognizing benchmarks which are limited by a few factors? Read on to find out ...

Is it Math? Chemistry?!

While it may seem that doing some mathematical manipulation on the graphs will give us the graph of a combination, such as adding the graphs, or multiplying the graphs. However, this is not the case. In order to predict the graph of a benchmark with multiple limitations we must analyze our combination benchmark like a chemical formula.. Chemistry? What's that got to do with it you may ask. The answer is the 'limiting reagent' concept.

WTF is a Limiting reagent?

In a chemical equation, i.e. the synthesis of a compound, for example, the limiting reagent is the substance which limits the amount of desired product. Even if there is 100 tons of the other substance in the reaction, the amount of desired product (i.e. not including excess) will remain the same. This is the idea behind predicting the results.

Geometry and Fill-Rate Limited

Both of these limitations cannot coexist, only at one point (i.e. a certain CPU speed). The graph of the results of a Geometry and Fill-rate limited benchmark can be expressed by the following split function.

                             {   k*CPUSpeed, 0<CPUSpeed < CPUSpeed @fill-rate limit

FPS (CPUSpeed) = {

                             {   MaxFillRate, CPUSpeed >= CPUSpeed @ fill-rate limit

As you can see, the function aboves' graph looks like the graph of a line until you hit the CPUSpeed at which it is both Geometry and Fill-rate limited (i.e. The Fill-Rate is the "LIMITING REAGENT" in this case) After we pass this Fill-rate limit, the results are always going to be the same, since we hit the limit, and excess CPU Speed isn't going to help us.

Bandwidth and Geometry or Fill-rate limited

Again, this problem involves finding the minimum reagent. The equation is listed below:

                             {   k*CPUSpeed, 0<CPUSpeed < CPUSpeed @Bandwidth Limit

FPS (CPUSpeed) = {

                             {   Bandwidth Limit, CPUSpeed >= CPUSpeed @Bandwidth Limit

An easier way...

Looking at these two functions you will notice that they are very similar, actually, almost identical. Why memorize these equations when there is an easier way to represent the frame rate of a benchmarking composed of N number of limitations? The reason I even bothered to do all that work above is to explain where I got the equations from. Now that you pretty much understand (hopefully) the idea, let's employ the limiting reagent idea to ANY number of limitations.

At any given CPUSpeed (from now on, referred to as 'X') Our given 'Y' is limited by the limitation which gives us the least FPS (at that X). Writing this in Math terms, the equation is

F(X) = Minimum ( Lim1, Lim2, Lim3, Lim4,..., LimN);

Where Lim# = The max FPS possible with the Limitation

The Example:

Let's draw a sketch (no numbers) the FPS vs CPUSpeed (F(X) vs X) graph of the results of some benchmark which is geometry limited at a certain range, fill-rate limited at another, and let us introduce a third limitation to make it more interesting. What is this third limitation. Well, we want a limitation which wont be a horizontal line one (since fill-rate is already) so we will make an arbitrary limitation (lets call it the "Windows" limitation) This "Windows" limitation will have a negative acceleration, so the graph of the FPS vs CPUSpeed of a totally "Windows" limited game will look like a parabola with the equation of -x^2 + k, where k is some constant detailing the maximum FPS possible with the "Windows" limitation. The graph is pictured below:

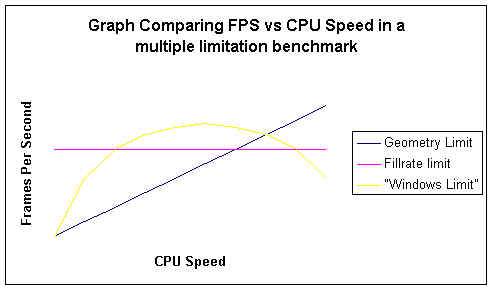
The graph which represents F(X) is the graph which consists of the Blue line until it intersects the Pink, then the pink until it intersects the yellow, and then the yellow until the "Windows" limitation becomes so great that the FPS reaches 0... (No hard feelings Microsoft :)

Conclusion

In conclusion, when choosing a 3D accelerator, it is helpful to know which benchmark results mean what, since benchmarks can be very misinforming if not interpreted correctly. Hopefully this article has given you some insight on how to interpret future benchmark results, like the ones Anand will be posting tomorrow (10/11/98)